Análise e Decodificação de Memória Flash NAND - Revelando a Dispersão ECC em Dispositivos Desconhecidos
Escrito por
Lucas Teske
em
Explorando memorias NAND
Quando em posse de um dispositivo a qual se deseja conhecer sobre, nem sempre é trivial o acesso ao conteúdo da memória flash. Devido a natureza das memórias NAND, é aplicado para todo conteúdo um algorítimo de correção de erros que pode causar uma ofuscação não intencional do conteúdo. Alguns fabricantes de processadores que controlam diretamente memórias do tipo NAND ou programadores de software “protegido” optam por customizar o jeito que estes algorítimos funcionam.
Neste artigo veremos como a estrutura básica de uma memória flash, por que a correção de erro existe e como identificar a dispersão do algorítimo de correção de erro usado.
Memórias Flash
As memórias flash têm se destacado como a espinha dorsal do armazenamento digital na era contemporânea. Presentes em dispositivos tão variados quanto SSDs, pen drives e cartões SD, estas memórias trazem uma combinação irresistível de rapidez, durabilidade e capacidade de retenção de dados mesmo na ausência de energia.
Historicamente, antes da ascensão das memórias flash, os principais dispositivos de armazenamento eram baseados em mídias magnéticas, como discos rígidos e disquetes, ou em memórias do tipo EPROM (Erasable Programmable Read Only Memory). Enquanto as mídias magnéticas possuíam partes móveis e eram mais propensas a falhas físicas, as EPROMs necessitavam de um processo de apagamento específico, tornando a regravação de dados um processo mais lento e menos eficiente.
Dentro da categoria de memórias flash, encontramos diferentes variações, com as versões NOR e NAND sendo as mais predominantes. Neste artigo, focaremos nas memórias flash do tipo NAND, reconhecidas por sua alta densidade de armazenamento e amplamente utilizadas em dispositivos de armazenamento cotidianos, garantindo velocidade e confiabilidade na leitura e gravação de dados.
Anatomia de uma Célula NAND
Diagrama detalhado de uma célula NAND
No coração da tecnologia de memória flash, encontra-se a intricada arquitetura de uma célula NAND. A ilustração acima delineia os componentes fundamentais da célula: o Control Gate, o Floating Gate, camadas isolantes de óxido, juntamente com os terminais N-Type Source e N-Type Drain, todos construídos sobre um substrato do tipo-P. Os bits são armazenados na memória flash retendo elétrons no Floating Gate.
Durante a operação de gravação, uma tensão é imposta sobre o Control Gate, induzindo elétrons a atravessarem a barreira de óxido e se alojarem no Floating Gate. Assim que os elétrons alcançam o Floating Gate, eles permanecem lá, denotando um estado “gravado”.
Para ler a informação armazenada, uma tensão é aplicada ao Control Gate. Se houver elétrons no Floating Gate, eles criarão uma força de repulsão, bloqueando a passagem de elétrons do Source para o Drain. Este estado é reconhecido como um bit “0”. Contudo, se o Floating Gate estiver desocupado, a corrente elétrica circulará sem impedimentos, correspondendo a um bit “1”.
Célula NAND no estado “gravado”
Finalmente, a configuração elétronica — seja sua ausência ou presença — determina se a célula está representando um bit “0” ou “1”. A imagem subsequente mostra uma célula no estado “apagado”, caracterizado pela livre circulação de elétrons entre os terminais.
Célula NAND no estado “apagado”
Arquitetura da Memória NAND
Diagrama representando a organização de um bloco NAND
A memória NAND é meticulosamente organizada em uma estrutura hierárquica. Começando pela menor unidade, temos a célula. Estas células são, por sua vez, agrupadas para formar páginas. Avançando na hierarquia, múltiplas páginas são então consolidadas para constituir um bloco, como ilustrado no diagrama acima.
Essa disposição estrutural não é apenas por organização. Ela desempenha um papel vital na eficiência das operações da memória flash. Um detalhe importante a se considerar é que, em diversos dispositivos baseados em tecnologia flash, a operação de apagamento é executada em nível de bloco, e não em células ou páginas individuais.
A imagem exemplifica uma memória NAND que contém páginas de 2048 bytes de dados acrescidos de 64 bytes destinados à correção de erro, totalizando 2112 bytes por página. Estas páginas estão agrupadas em blocos que abrigam 64 páginas cada, resultando em 128K bytes de dados e 4K bytes para correção.
Os bytes adicionais em cada página não são meros complementos. Eles são intrínsecos à integridade da memória. Embora sejam armazenados da mesma forma que qualquer outro byte, muitas vezes são alocados para funções específicas, como paridade em algoritmos de Correção de Erros (ECC). Essa correção é indispensável, pois, durante a fabricação ou mesmo ao longo do uso, é possível que algumas células da memória NAND apresentem defeitos ou se desgastem, comprometendo a precisão dos dados armazenados. O ECC, portanto, atua como uma camada protetora, assegurando a confiabilidade dos dados mesmo diante de imperfeições na memória.
Lendo memórias Flash
Ao lidar com leitura e gravação em memórias Flash, existe uma variedade de dispositivos disponíveis. Para memórias flash com encapsulamentos menos convencionais, como o BGA (Ball Grid Array), frequentemente recorro ao programador RT809H, utilizando um adaptador específico para tal encapsulamento. A memória flash em questão foi originalmente extraída de um equipamento da PAX, um modelo disponível no Mercado Livre sob a descrição “máquina de cartão”. Vale destacar que o tipo de encapsulamento dessa memória flash é BGA63, indicando um arranjo de 63 pinos no formato ball-grid-array.
Memória Flash no programador universal RT809H pronto para leitura
Após a extração dos dados da memória flash, um passo fundamental é a utilização da ferramenta binwalk. Este comando tem a função de vasculhar e listar possíveis assinaturas de arquivos conhecidos contidos no dump da memória, permitindo uma análise preliminar de seu conteúdo. Essa etapa é crucial para discernir se enfrentaremos desafios ao tentar decifrar os dados armazenados, como no caso de estarem criptografados.
É importante ressaltar que a imagem produzida pelo programador RT809H retrata o conteúdo da memória flash em seu estado mais puro, sem qualquer filtragem. Isso significa que os bits de paridade do ECC (Error-Correcting Code) estão inclusos. Esta característica pode introduzir nuances durante a análise, pois nem todas as assinaturas serão reconhecidas de maneira acurada, principalmente se considerarmos arquivos que podem iniciar no final de uma página de memória.
$ binwalk F59L1G81MA@BGA63_1111.BIN
DECIMAL HEXADECIMAL DESCRIPTION
--------------------------------------------------------------------------------
438548 0x6B114 Base64 standard index table
(...)
3514378 0x35A00A PC bitmap, Windows 3.x format,, 320 x 240 x 24
7839754 0x77A00A uImage header, header size: 64 bytes, header CRC: 0x538F3DE9, created: 2021-05-27 08:14:51, image size: 3696472 bytes, Data Address: 0x80800000, Entry Point: 0x80800000, data CRC: 0xA22F74A5, OS: Linux, CPU: ARM, image type: OS Kernel Image, compression type: none, image name: "Linux-2.7.93.9707R"
7839818 0x77A04A Linux kernel ARM boot executable zImage (little-endian)
7857081 0x77E3B9 gzip compressed data, maximum compression, from Unix, last modified: 1970-01-01 00:00:00 (null date)
(...)
20815882 0x13DA00A uImage header, header size: 64 bytes, header CRC: 0xF95F6882, created: 2021-05-27 08:20:25, image size: 8185419 bytes, Data Address: 0x83800000, Entry Point: 0x83800000, data CRC: 0xE5674944, OS: Linux, CPU: ARM, image type: RAMDisk Image, compression type: none, image name: "RAMDISK-2.7.93.9707R"
(...)
20815946 0x13DA04A gzip compressed data, maximum compression, from Unix, last modified: 2021-05-27 08:20:23
33792010 0x203A00A uImage header, header size: 64 bytes, header CRC: 0x588DFFBC, created: 2021-05-27 08:19:13, image size: 6412038 bytes, Data Address: 0x0, Entry Point: 0x0, data CRC: 0x32979F1E, OS: Linux, CPU: ARM, image type: Firmware Image, compression type: none, image name: "BASE-2.7.93.9707R"
33792074 0x203A04A gzip compressed data, maximum compression, from Unix, last modified: 2021-05-27 08:19:11
46768138 0x2C9A00A UBI erase count header, version: 1, EC: 0x3, VID header offset: 0x800, data offset: 0x1000
A avaliação da entropia é uma técnica eficaz para detectar conteúdo criptografado ou compactado em uma memória. Quando falamos de entropia em dados, estamos nos referindo à quantidade de informação ou imprevisibilidade contida nesses dados. A ferramenta binwalk oferece um modo específico para medir essa entropia.
Arquivos que estão compactados ou criptografados tendem a exibir um padrão de dados aparentemente aleatório, resultando em uma medida de entropia que se aproxima de 1. Em contraste, arquivos “plain-text” ou dados não codificados geralmente possuem entropia significativamente mais baixa, tendendo para valores próximos de 0, pois seu conteúdo é mais previsível.
Para explorar essa funcionalidade no binwalk, utiliza-se a opção -E, que ativa o modo de medição de entropia. Ao executá-la, você receberá um gráfico que visualmente representará as variações de entropia ao longo do arquivo, facilitando a identificação de segmentos criptografados ou compactados.
$ binwalk -E F59L1G81MA@BGA63_1111.BIN
DECIMAL HEXADECIMAL ENTROPY
--------------------------------------------------------------------------------
0 0x0 Falling entropy edge (0.027839)
7880704 0x784000 Rising entropy edge (0.995063)
12345344 0xBC6000 Falling entropy edge (0.000000)
20869120 0x13E7000 Rising entropy edge (0.997811)
29257728 0x1BE7000 Falling entropy edge (0.000000)
33824768 0x2042000 Rising entropy edge (0.999076)
40386560 0x2684000 Falling entropy edge (0.372003)
47253504 0x2D10800 Falling entropy edge (0.725862)
62879744 0x3BF7800 Falling entropy edge (0.737729)
67244032 0x4021000 Rising entropy edge (0.966013)
67311616 0x4031800 Falling entropy edge (0.776734)
69611520 0x4263000 Falling entropy edge (0.790624)
69679104 0x4273800 Rising entropy edge (0.972091)
69814272 0x4294800 Falling entropy edge (0.836573)
70322176 0x4310800 Falling entropy edge (0.844177)
72689664 0x4552800 Falling entropy edge (0.643195)
74008576 0x4694800 Falling entropy edge (0.783870)
74584064 0x4721000 Falling entropy edge (0.471472)
75259904 0x47C6000 Falling entropy edge (0.787818)
76613632 0x4910800 Falling entropy edge (0.823394)
76748800 0x4931800 Falling entropy edge (0.687502)
82837504 0x4F00000 Falling entropy edge (0.360502)
84291584 0x5063000 Falling entropy edge (0.775172)
84934656 0x5100000 Falling entropy edge (0.714603)
95385600 0x5AF7800 Falling entropy edge (0.788762)
103233536 0x6273800 Falling entropy edge (0.775540)
104992768 0x6421000 Falling entropy edge (0.750242)
124475392 0x76B5800 Falling entropy edge (0.281623)
125253632 0x7773800 Falling entropy edge (0.750710)
133507072 0x7F52800 Falling entropy edge (0.798972)
137566208 0x8331800 Falling entropy edge (0.768062)
137701376 0x8352800 Falling entropy edge (0.743758)
Entropia da Imagem Lida
No gráfico de entropia apresentado, as áreas de alta entropia se destacam como picos que se aproximam do valor 1 no eixo vertical. Estas regiões apontam para trechos de dados que têm uma distribuição que parece aleatória de bits, o que é típico de dados compactados ou criptografados.
Ao cruzar a posição destes picos com as informações fornecidas pelo comando binwalk, conseguimos entender a natureza destes segmentos de alta entropia. No nosso caso, os pontos de alta entropia correspondem a partes compactadas, e não a dados criptografados. Essa dedução fica clara quando vemos que o binwalk identificou assinaturas relacionadas a dados compactados com gzip nas posições indicadas.
O fato de reconhecer essas assinaturas mostra claramente que o conteúdo, apesar de compactado, não está criptografado. Se fosse, o binwalk não teria identificado essas assinaturas, pois os dados criptografados se parecem com um monte de informações aleatórias, sem padrões específicos. Então, olhando tanto o gráfico de entropia quanto as informações do binwalk, conseguimos uma boa ideia da estrutura e tipo dos dados na memória flash analisada.
Quando a dispersão do ECC não é padrão
Para garantir que os dados sejam acessados de forma precisa, é fundamental excluir os bits de paridade inseridos em cada página de memória. Supondo que os últimos 64 bytes de cada página sejam alocados para o ECC, podemos criar um script Python que lê os 2112 bytes (representando a página completa de memória) e grava somente os 2048 bytes correspondentes ao dado puro, desconsiderando o ECC, em um novo arquivo.
#!/usr/bin/env python
f = open("F59L1G81MA@BGA63_1111.BIN", "rb")
o = open("FIXEDDATA.bin", "wb")
pagesToRead = 65536
for i in range(pagesToRead):
page = f.read(2112)
data = bytearray(page[:2048]) # Nuke ECC
o.write(data)
f.close()
o.close()
Com os dados agora limpos, a próxima etapa é identificar os arquivos presentes para verificar a eficácia da nossa suposição. Uma olhada rápida na lista de arquivos destacados pelo binwalk nos fornecerá uma indicação.
$ binwalk F59L1G81MA@BGA63_1111.BIN
DECIMAL HEXADECIMAL DESCRIPTION
--------------------------------------------------------------------------------
438548 0x6B114 Base64 standard index table
439650 0x6B562 DES PC1 table
439738 0x6B5BA DES PC2 table
440945 0x6BA71 DES SP2, little endian
441738 0x6BD8A DES SP1, little endian
477666 0x749E2 Certificate in DER format (x509 v3), header (...)
478540 0x74D4C Object signature in DER format (PKCS header (...)
479065 0x74F59 Object signature in DER format (PKCS header (...)
1384724 0x152114 Base64 standard index table
1385826 0x152562 DES PC1 table
1385914 0x1525BA DES PC2 table
1387121 0x152A71 DES SP2, little endian
1387914 0x152D8A DES SP1, little endian
1423842 0x15B9E2 Certificate in DER format (x509 v3), header (...)
1424716 0x15BD4C Object signature in DER format (PKCS header (...)
1425241 0x15BF59 Object signature in DER format (PKCS header (...)
3514378 0x35A00A PC bitmap, Windows 3.x format,, 320 x 240 x 24
7839754 0x77A00A uImage header, header size: 64 bytes, header (...)
7839818 0x77A04A Linux kernel ARM boot executable zImage (litt(...)
7857081 0x77E3B9 gzip compressed data, maximum compression, (...)
(...)
Podemos identificar um bitmap logo no começo da imagem, onde o binwalk consegue inclusive identificar o tamanho e profundidade de bits dele:
3514378 0x35A00A PC bitmap, Windows 3.x format,, 320 x 240 x 24
Uma característica marcante dos bitmaps é a forma como armazenam informações de cores. Os bytes no arquivo mapeiam diretamente para as cores da imagem. Assim, quando temos uma região da imagem que apresenta uma única cor, essa cor é representada por sequências consecutivas de bytes idênticos no arquivo. Essa propriedade é especialmente útil quando tentamos discernir a distribuição dos bits de correção de erro (ECC). Se um segmento do bitmap, que se ajusta a uma página de memória, exibe a mesma cor que outro segmento em uma página diferente, é esperado que seus bits de ECC correspondentes sejam idênticos.
Considerando que a imagem identificada possui uma profundidade de cor de 24 bpp (bits por pixel), cada pixel é representado por 3 bytes. Dada a capacidade de uma página de memória ser de 2048 bytes, isso se traduz em cerca de 682 pixels por página. Isso é ligeiramente mais do que duas linhas da imagem. A tentativa de acessar o bitmap na sua forma atual sugere inconsistências, o que nos leva a questionar nossas suposições iniciais sobre a distribuição dos bits de ECC.
Logotipo corrompido da PAX
Para uma interpretação adequada, é vital extrair várias páginas da memória contendo os dados do bitmap de forma alinhada. Dessa forma, podemos ter certeza de que a cada intervalo de 2112 bytes, estamos lidando com uma nova página, e não uma continuação da anterior. Posteriormente, podemos utilizar um software de edição de imagem que permita manipular imagens em formatos “RAW” arbitrários. Neste contexto, utilizaremos o GIMP para analisar os dados crus da imagem. Uma das vantagens do GIMP é a flexibilidade em definir a geometria da imagem e a formatação dos pixels.
Para facilitar a identificação dos bits de ECC, definiremos a largura da imagem como 2112, correspondendo ao tamanho da página de memória. Isso permitirá visualizar cada página de memória como uma linha distinta. Vamos escolher uma representação de 8 bits por pixel, em tom monocromático, para garantir uma correspondência exata de 2112 bytes por linha. Em relação à altura, optaremos por, no mínimo, 100 linhas, de modo a proporcionar uma visão clara das variações entre as diferentes páginas de memória.
Ao examinar a representação visual fornecida pelo GIMP, notamos segmentos claramente definidos de 512 bytes dentro de cada página de memória. Esses segmentos são intercalados com colunas mais finas, cuja aparência parece diretamente influenciada pelo bloco adjacente.
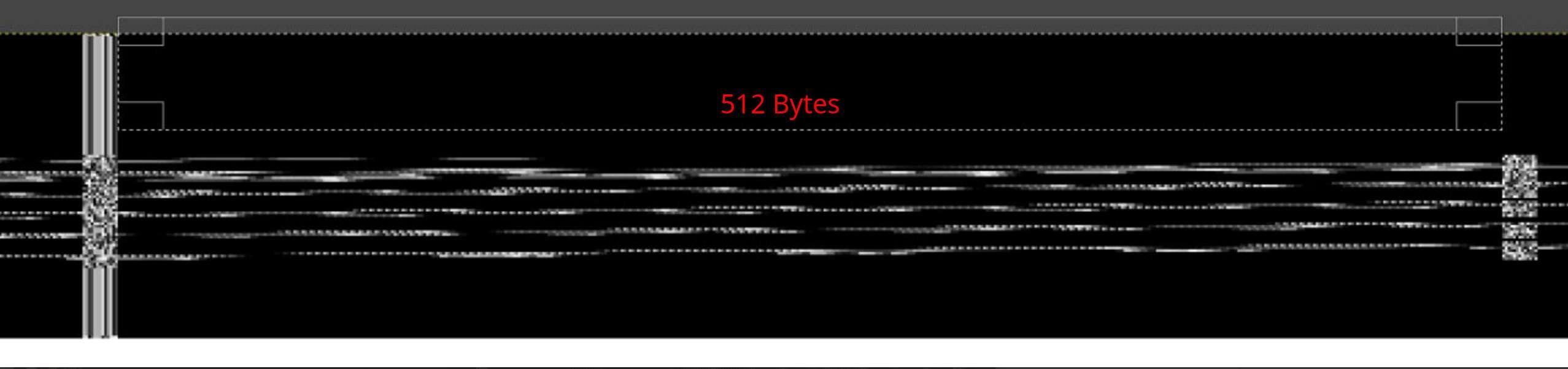Blocos de 512 bytes
Observando mais atentamente, percebemos que as linhas completamente pretas apresentam uma coluna com padrões consistentes à esquerda da marcação de 512 bytes. Contrapondo-se a isso, linhas que exibem alguma variação também manifestam discrepâncias nessa mesma coluna à esquerda. Com base nessa observação, podemos inferir que as colunas posicionadas tanto à esquerda quanto à direita do segmento de 512 bytes representam, de fato, dados de paridade, e não são parte intrínseca do bitmap. Isso se torna ainda mais evidente considerando que as primeiras linhas do bitmap são inteiramente pretas.
Ao considerar a página de memória em sua totalidade, outro detalhe se destaca: apesar do padrão observado, há uma coluna completamente branca em uma posição inesperada. Além disso, a primeira coluna, que teoricamente deveria ser branca, parece estar deslocada ou alterada de alguma forma.
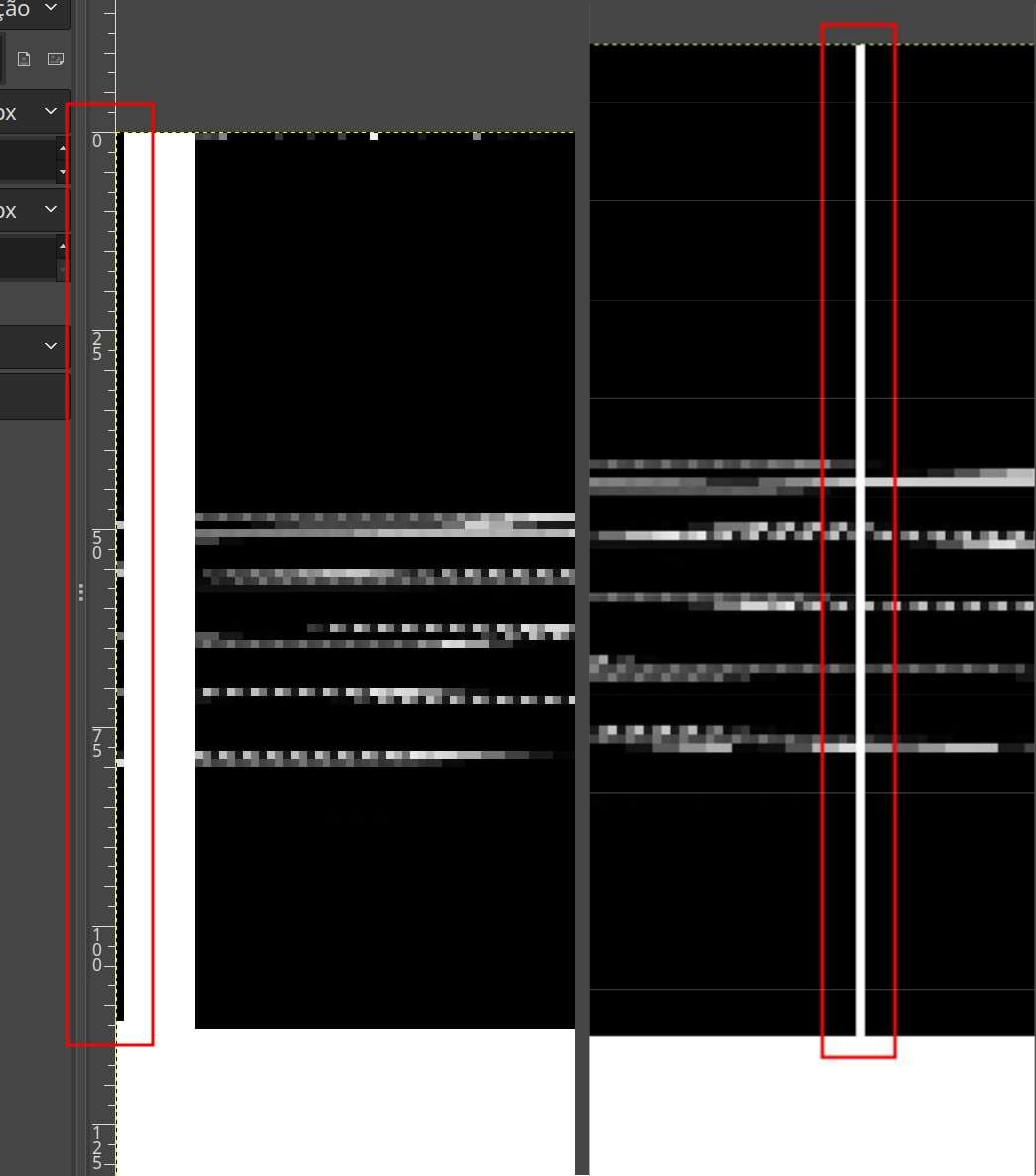Coluna aparentemente trocada de lugar
A hipótese levantada sugere que, por alguma razão, essas colunas podem ter sido trocadas de lugar durante o processo de dispersão. Para validar essa suposição, uma abordagem prática seria utilizar o próprio GIMP para reposicionar a coluna e avaliar se o conteúdo resultante se alinha de forma harmoniosa com o restante da página de memória.
Trocando colunas identificadas de local
A imagem acima valida nossa conjectura, destacando que a realocação das colunas proporciona uma visualização mais coerente do conteúdo. Embora pareça incomum à primeira vista, considerando a natureza de segurança do dispositivo, é plausível pensar que essa disposição alterada possa ser uma forma deliberada de esconder dados. Essa peculiaridade não é mencionada em nenhuma documentação pública disponível para o processador do dispositivo.
Com base nessas descobertas, temos as ferramentas necessárias para aprimorar nosso script em Python, visando eliminar os bits de paridade e rearranjar os segmentos de 512 bytes, com o objetivo de obter uma imagem refinada e coerente.
#!/usr/bin/env python
f = open("F59L1G81MA@BGA63_1111.BIN", "rb")
o = open("FIXEDDATA.bin", "wb")
pagesToRead = 65536
for i in range(pagesToRead):
page = f.read(2112)
data = bytearray(page[10:10+512] + page[535:535+512] + page[1060:1060+512] + page[1585:1585+512])
data[len(data)-48-1] = page[0]
o.write(data)
f.close()
o.close()
Após todos os passos de análise e correção, conseguimos extrair o bitmap e validar que todas as nossas hipóteses e métodos de análise estavam corretos:
Logotipo “ajustado” da PAX
Conclusão
É essencial destacar que nossa abordagem se limitou a remover os bits de paridade, sem aplicar de fato o algoritmo de correção de erros. Como mencionado anteriormente, as memórias flash, particularmente as do tipo NAND, podem apresentar bits defeituosos, inclusive desde sua fabricação. A omissão do algoritmo de ECC específico pode resultar em inconsistências nos dados finais.
Por sorte, o conteúdo deste dispositivo específico não estava criptografado, o que nos facilitou na análise de dispersão, aproveitando-se apenas de um conteúdo conhecido. Se o conteúdo estivesse criptografado, seria essencial identificar um padrão recorrente (como páginas de memória vazias) onde a informação de ECC estaria gravada.