The Parallella Board and HyperSignal

I’ve got my Parallella board a few months ago (at Campus Party Brazil of 2014 to be exact). I’ve already studyied the Epiphany Processor ManyCore Architecture before, and I was excited to get one of those boards at my hand.

The first thing I imagine to do, is a Matrix Upscaler Interpolator for my project HyperSignal (its offline now, but I will get it online soon and code at github) because the simple nature of a interpolation algorithm drops all the overhead of multithreading over the memory controller, that has limited number of simultaneous access and also depends on how the operating system manages that.

So I have in my mind the old timings that I usually take for rendering the Image tiles (the matrix upscaled). I had about a 8 milion matrix componentes to be upscaled on Google Maps Tiles. Obviously each Google Maps Tiles only use a few hundred of values for upscaling. So it was about 5600 tiles and was taking about 5 hours to do that in a i7 980 running at 6 threads 3.2GHz, 24GB of DDR3 RAM @ 1333MHz. That was really concerning me because of the speed, 5 hours for just 5 thousand tiles. That was basicly just my city signal overlay (São Paulo).

I was also aware that this problem is very very easy to scale. Since there is individual tiles that doesnt rely on their neighboars. So I could easily take over 100 computers and reduce 1/100 of the time. But that would be expensive and also consumes a lot of power (My i7 was consuming 400W to do that work).

And them, the Parallella Board got my attention in their early notice on the internet ( I think in 2012 or 2013 they was announced), so I decided to give a try. Even with the HyperSignal being just a Mathematics Study for me, messing with that board would also get a good knowledge for me.

But I got busy and them just few weeks I managed to get time to mess with it.

Starting the programming

The HyperSignal project has been shutdown in middle of 2013, mostly because the VPS Service (Hostlocation) has lost ALL of my data including the backups. Now I learned that I should make a backup with another company also. But I still have the most recent program files, I’m just dont have that 8M matrix database. But okay, I dont need it to test it.

So the original interpolation code an NxM sample matrix and upscales to WxH tile matrix using a python script to fetch the necessary data from database, organizing the threads and the Weaver Module to do the interpolation in native code. It also was blurring the output matrix to remove few artifacts from the optimization that I did.

I had two options of interpolation: Bilinear and Bicosine. Bicosine gets a result near of Bicubic interpolation, but its A LOT faster. Also since the HyperSignal fetches the data using GPS and GPS doesnt have a lot of precision (usually 2.5 meters or more), the bicosine was OK. So we have that two mathematics formula:

Bilinear

Having f(x,y) as sample lookup if x and y are integers, and

   

for non integers

Bicosine:

Having mw as matrix width, f(x,y) as sample lookup for integer x and y,

   

   

   

   

   

   

   

   

   

for non integer x,y.

CF = CosineFactor, CI = CosineInterpolate

So I made a few helper functions in C based on my previous work:

unsigned char bilinear(const unsigned char *data, double x, double y, int mw)	{
	int rx = (int)(x);
	int ry = (int)(y);
	float fracX = x - rx;
	float fracY = y - ry;
	float invfracX = 1.f - fracX;
	float invfracY = 1.f - fracY;

	unsigned char a = val(data,rx,ry,mw);
	unsigned char b = val(data,rx+1,ry,mw);
	unsigned char c = val(data,rx,ry+1,mw);
	unsigned char d = val(data,rx+1,ry+1,mw);

	return ( a * invfracX + b * fracX) * invfracY + ( c * invfracX + d * fracX) * fracY;
}

inline double cosineInterpolate(double y0, double y1, double mu)	{
	double mu2 = (1-cos(mu*M_PI))/2;
	return (y0*(1-mu2)+y1*mu2);
}

unsigned char bicosine(const unsigned char *data, double x, double y, int mw)	{

	double baseX	=	floor(x);			//	X Integer Part
	double baseY	=	floor(y);			//	Y Integer Part
	double fracX	=	x - baseX;			//	Fraction Part of X
	double fracY	=	y - baseY;			//	Fraction Part of Y

	double y0		=	baseY;			//	Previous Y value
	double y1		=	baseY+1;		//	Next Y value
	double x0		=	baseX;			//	Previous X value
	double x1		=	baseX+1;		//	Next X value

	//	Find c0 = f(x0,y0)  and c1 = f(x1,y0)
	unsigned char c0 = val(data, y0, x0, mw);
	unsigned char c1 = val(data, y0, x1, mw);

	//	Find c2 = f(x0,y1) and c3 = f(x1,y1)
	unsigned char c2 = val(data, y1, x0, mw);
	unsigned char c3 = val(data, y1, x1, mw);

	//	Interpolate from c0 to c1 to find top = f(fracX,y0)
	double top	=	cosineInterpolate((double)c0,(double)c1,fracX);

	//	Interpolate from c2 to c3 to find bottom = f(fracX,y1)
	double bottom	=	cosineInterpolate((double)c2,(double)c3,fracX);

	//	Interpolate from top to bottom to find f(x,y)
	return cosineInterpolate(top,bottom,fracY);

}

I will not post the entire code here, it will be soon on github.That pieces of code are just for reference when I talk about Epiphany Performance Issues I had.

So for the Host program I did use PThreads for threading. So since I have limited RAM on Epiphany, I need to make a compile time variables to set how much memory the thread can use. The biggest memory use will be on the output matrix, that on my case should be 256×256. Since this would take 65k of unsigned chars, I couldnt fit on only one epiphany core. For that, I made a Work Struct with a compile time Defines for Sample Width and Height and Output Width and Height. Also I set deltas and scale variables so I could split a tile in many and make each core process a piece of the tile. I decided to give a try with 128×128 matrix, that would use 16KB of memory, and should fit nicely on Epiphany Core RAM. So here is my work struct:

#define SAMPLE_WIDTH 8
#define SAMPLE_HEIGHT 8

#define OUTPUT_WIDTH 128
#define OUTPUT_HEIGHT 128

#define SAMPLE_SIZE (SAMPLE_WIDTH * SAMPLE_HEIGHT)
#define OUTPUT_SIZE (OUTPUT_WIDTH * OUTPUT_HEIGHT)

#define CURRENT_POS (0x2000)

#define NUM_WORKS 4
#define BUF_SIZE 32

#define ALIGN8 8

typedef struct __attribute__((aligned(ALIGN8))) {
   int workid;							//	Work ID
   float x0, y0;						//	Coordinates
   float sx, sy;						//	ScaleX and ScaleY
   unsigned char sample[SAMPLE_SIZE];				//	Origin Matrix
   unsigned char output[OUTPUT_SIZE];				//	Output Matrix
   unsigned char done;						//	Done Flag
   unsigned char error;						//	Error Flag
   int coreid;							//	Core ID
} HSWork;

So I could use this as a message between HOST<>THREADS or HOST<>EPIPHANY with only allocating an array of HSWork and telling the threads/epiphany for looking on a specific index. Then after all threads finish their works, I can just run a consolidation of data on the host side.

Testing

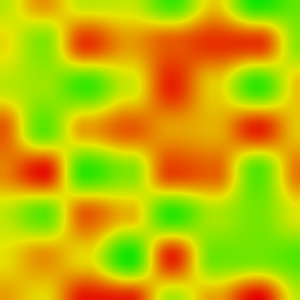
For testing I initialized an 8×8 Sample Matrix and made it output to a 384×384 Matrix. I made a python program to convert the resulting unsigned char matrix to a colorized one just for reference. I’m not couting the performance of the python app, just the interpolation part. Also I’m just couting the work and consolidation time, not the open/close apps overhead.

The sample matrix used in this test was that:

unsigned char Data[] = {
	157,83 ,153,147,223,114,248,200,
	120,185,30 ,86 ,50 ,28 ,29 ,180,
	153,169,225,146,20 ,115,229,108,
	50 ,206,89 ,51 ,89 ,99 ,19 ,112,
	74 ,9  ,232,185,36 ,54 ,210,66 ,
	151,206,52 ,100,232,163,191,135,
	125,81 ,122,246,20 ,197,194,210,
	87 ,122,11 ,16 ,163,90 ,1  ,152
};

And the color output is that:

So for the performance test, I ran about 100 tests on my notebook (An Intel(R) Core(TM) i7-3630QM CPU @ 2.40GHz with 16GB DDR3 Ram with Ubuntu Linux 14.04 3.12.0-7-generic kernel)  and take an average value from them. The work as SINGLE THREAD did the job (single 384×384 output matrix) in 17ms. For a 4 threads mode with 128×128 slices, it took 28ms for ending the job. Also my notebook computer is taking about 150W to do the job.

That values proves me one thing: The overhead of my algorithm is exactly at memory access. Since I cannot explicity set the output to be on CPU Cache, the entire output matrix and sample matrix are on RAM. Even on my Quad Channel Memory Controller, it doubled the work time. So probably my linux kernel isnt managing the memory couting the quadchannel controller. To be honest, I dont know if the linux kernel even know that is a multichannel memory controller. Maybe the CPU Abstracts that for the kernel.

Ok, so now its time to get on Parallella Board!

Programming on Parallella Board and First Impressions

So I started my work for Parallella Board. First thing I was trying to make a good communication between the Epiphany core and the Host Program. I noticed that few people maps directly at one defined address. Like if the Epiphany has 0x0 to 0x7FFF memory address range, just picking one start address on this range and assuming that is your variable. So you could use e_read/e_write on the host to write directly on it. This works fine for small variables (like an int) if you keep out the IVT (first 64 bytes of the memory) and out of the C Stack (usually at end of the address space), but for long data like my work, it is a problem. Since linker doesnt know that I’m mapping this address, it could place something important there, or even replace your data. So for solving this, you would need to make a custom linker script to explict say that you have some data there.

I dont know much about compiler stuff, so I was trying to find a different approach. On the Parallella Board you have a 32MB isolated memory that is on the 1GB DRAM, but not mapped inside linux kernel. So basicly, its an unmanaged 32MB RAM Space. Adapteva’s team did that for using that 32MB for shared data between host and epiphany, since both can access the address space. So I have a big space there, with limited throughput because of that is on the same memory that host OS is running, but a good space for storing input/output data. So I decided to do that:

1. On the host program initializes an array of HSWork
2. Put the Sample, Scales, Coordinates at each work
3. Copy that initialized array of work to Shared DRAM Space
4. Initializes and start the Epiphany cores
5. Wait for all cores finish their works
6. Read all works from Shared DRAM to local program
7. Consolidate the data
8. Save and exit

and on the epiphany side:

1. Pre-allocated HSWork space at internal RAM, defined on the code. So linker will notice its existence.
2. Determine the relative X,Y coords of the core and the work number
3. Copy from Shared DRAM the HSWork data to Pre-allocated local HSWork
4. Do the work
5. Write the HSWork data (now with output filled) to Shared DRAM
6. Exit

So with that approach, I will have the best work performance my C Algorithm would do. Also it would use only the minimum writes/reads from Shared DRAM on both sides.

Testing the Epiphany Program and Performance Issues

So as usual, on the first test I just ran and I got scared: It too 10 seconds to finish the work! That was VERY strange. I was expecting it to be slower than my computer (since my processor runs at 3GHz not 667MHz) but not THAT slower. So I made this post at Parallella Community Forums: http://www.forums.parallella.org/viewtopic.php?f=23&t=1780

But I solved the problem just before anyone presented a solution. So the biggest problem was one GCC *bug* (not really a bug, but for e-gcc could be considered one) that all floating point operations was default to double. The Epiphany (at least current one) has a Single Precision Float Point Unit, and for making double precision calculations, it need to split the data and do a lot of operations to get the result. Basicly is doing all by software and not hardware. That is REALLY slow, and was taking a lot of milliseconds to do an operation. So all constant values I had on Float operations I put the prefix .f , like if I had 2.0 value, I put 2.f or 2.0f. That enforces the var to be Float not Double. This reduced the time from 10 seconds to 120ms!

Also another thing I did to improve more the peformance: Remove all divisions that I could. I had many constants operations like x / 2.f or so. Divisions are slower than multiplications ( see here http://stackoverflow.com/questions/15745819/why-is-division-more-expensive-than-multiplication ), but for Epiphany its about 3.5 times slower than a equivalent multiply. So just changing x / 2.f to x * 0.5f would reduce 3.5x the time to do that operation. So I started to review all my formulas and trying to isolate the constants to calculate at compile time (or one time before the interpolation loop). I also added -O3 optimization flag. So in the end I got an work running at impressive 50ms!

One good thing to metion, I needed to use 4 cores to build a 256×256 tiles, so this is only 1/4 of the Epiphany E16 chip. But if I build 4 tiles, it takes EXACTLY the same time 50ms time to do all the 4 tiles! That means my work algorithm is very good for scaling up on epiphany! 😀

So since I got a reduction of about 70% of runtime just by optimizing the formulas, I ported the code also to the first version with multithreading. Doing so, made it drop from 17ms on single thread to 10ms, and from 28ms on multithreading to 20ms.

Conclusion

So, what that values mean? Epiphany is good for HyperSignal Tile Maker? Lets revise the data we got in best cases:

1. On PC: 10ms – 150W
2. On ARM: 60ms – 3W
3. On Epiphany: 50ms – 2W

So you are probably thinking: PC ROCKS! – But I need to say: No, PC Sucks.

Why? Raw performance is not the only factor I’m considering (and also not the only you should). My notebook is really 6 times faster than epiphany, but it consumes a LOT more power. So lets make a rate to define the quality. Since higher tiles per sec we can do with less watts is good, lets do an rate. Lets first calculate how much tiles/sec we can do on each plataform:

1. On PC: 10ms per tile, so 100 tiles/sec
2. On ARM: 60ms per tile, so 16 tiles/sec
3. On Epiphany: 50ms per tile, so 20 tiles/sec

Ok so, but this data isnt really correct. All of these plataforms can do more than one tile in parallell right? Yeah, right. Lets do a table for simultaneously work:

1. On PC: 28ms per 4 tile, so 7ms per tile, so 142 tiles/sec
2. On ARM: 100ms per 2 tile, 50ms per tile, so 20 tiles/sec
3. On Epiphany: 50ms per 4 tile (on 16 core), so 80 tiles/sec

So we have the data. So epiphany is now more close to the PC. That is pretty impressive, but there is the power factor to consider too! So lets divide the Tiles Per Second Rate by the Power.

1. On PC: 142 tiles/sec on 150W – 0,94 Tiles/Second/Watt
2. On ARM: 20 tiles/sec on 3W – 6,6 Tiles/Second/Watt
3. On Epiphany: 80 tiles/sec on 2W – 40 Tiles/Second/Watt

So WOW, epiphany ROCKS A LOT on Power Performance! So there is anything more we should consider? Yes there are a few.

The first thing is, I’m not fair with the i7 guy. My notebook is running a lot of stuff (cdrom, LCD Screen, GPU Card ) and many things that isnt on the use of the program but is taking power. Just the standby power of my notebook is about 100W, so the pure i7 would do better.

So considering that, we need to have another way to compare. The best way is using the ARM processor on the Parallella Board, it is an ARM but has similarities with an common x86 Desktop. It does few things faster, other things slower, but its more fair to consider. So considering just the ARM and Epiphany we have a 40 to 6,6 performance at about the same power.  That means the performance of epiphany for that application requires about 6 times less power than a ARM based one. Thats really impressive !

Final considerations

For the final considerations I should mention: I’m also using a 16 core Epiphany, that consumes a lot of power comparing to the new 64 core one. To be fair, both consume about the same power, but 64 cores … does have 64 core. So since my program scalates easy on epiphany without overhead (because of the epiphany arch) I could easily expand to 64 core version. So for a 64 version I would have 4 times faster processor for the SAME power. That menas 160 Tiles / Second / Watt that gives me 160 / 6,6 performance over the arm, or 24X faster operation with the same power. That is **** fast !

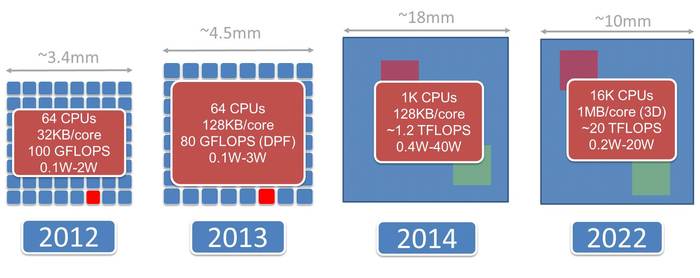
Also according to below pic ( Source: https://www.kickstarter.com/projects/adapteva/parallella-a-supercomputer-for-everyone ), there are 1024 core processor to start be planning in this year. They plan to make that 1024 core run on 40W.

What does that mean? It means since we have 1/4 tile per core, we have 256 tiles done in the same time, so we will have:

256 tiles in 50ms each. So 5120 tiles per sec. At 40 W we will have 256 tiles / sec / watt. The DOUBLE  performance per watt that 64 core have! That means all algorithms that run on Epiphany processor would have an headroom to be more complex along the time passes. This is really nice, because we are in a Bootleneck in currect archs so adding cores to x86 processors wont make they run faster.

So I got more impressed than I was when they launched. Its really nice to get one of these at hands, and I cant wait to get the 64 core version, the 1024 core, and all of that they launch!

Good luck Adapteva guys, making our future! 😀

---

---